1.    PARALELISMO Y PERPENDICULARIDAD

 

1.1.          TEOREMA DE LAS TRES PERPENDICULARES:

 

 

 

Si dos recta r y s son perpendiculares en el espacio y una de ellas por ejemplo la s es paralela a un plano α, sus proyecciones r’ y s’ también lo serán.

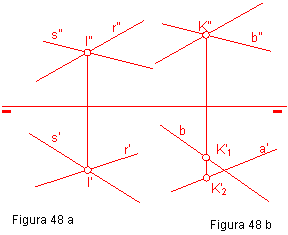
1.2.            INCIDENCIA ENTRE RECTAS.

 

Para que dos rectas r y s se corten en el espacio, las proyecciones homónimas del punto de intersección I  ( I’- I”) han de estar en una misma perpendicular a la línea de tierra. Figura 48a.

 

En caso contrario, las rectas se cruzarán en el espacio. Figura 48 b.

1.3.           PARALELISMO ENTRE RECTAS

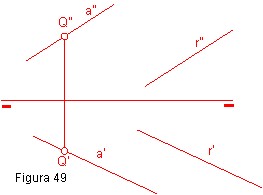
Si dos rectas son paralelas en el espacio, sus proyecciones también lo son. Figura 49.

 

Ejercicio: Trazar por un punto Q, una recta paralela a la recta r.

 

Bastará con trazar por el punto Q’-Q”, dos rectas a’-a”, paralelas a r’-r”.

1.4.PARALELISMO ENTRE PLANOS

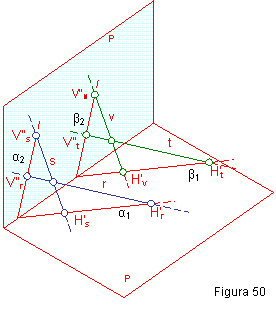
Para que un plano β sea paralelo a otro α, el primero debe contener a dos rectas t y v, paralelas a otros dos s y t contenidas en el plano α.

Como las trazas del plano son rectas del mismo, bastará con que estas sean paralelas.

 

 

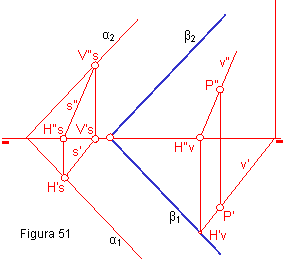
1.5.           TRAZAR POR UN PUNTO P UN PLANO β PARALELO A OTRO DADO α.

 

1. Se hace contener en el plano α una recta cualquiera por ejemplo la recta s.

 

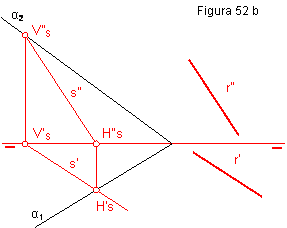
2.- Se traza por el punto P, una recta paralela a s. La traza horizontal del plano pasará por H’v y será paralela a α_1. Figura 51.

1.6.          PARALELISMO ENTRE RECTA Y PLANO

 

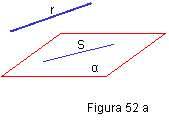Una recta  r es paralela a un plano  α cuando este contiene a una recta  s paralela  a la r dada. Figura 52a y b.

 

1.7.           DETERMINAR LAS TRAZAS DEL PLANO α QUE CONTENIENDO A LA RECTA r SEA PARALELO A OTRA RECTA s.

 

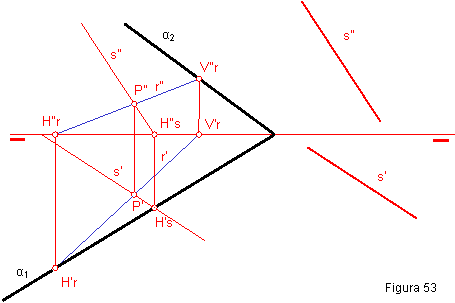
1. Por un punto  P cualquiera de la recta r, trazamos

una recta paralela a la dada s.

 

2. Seguidamente hallaremos el plano que  contenga a ambas rectas. Figura 53.

1.8.            PERPENDICULARIDAD ENTRE RECTA Y PLANO.

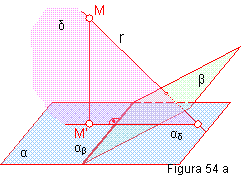
Si una recta r y un plano β son perpendiculares, lo serán a todas las rectas contenidas en el plano, siendo la traza del mismo una de ellas.

 

El plano proyectantes δ que contiene a la recta  será perpendicular a α y  β y por tanto la recta α_β y α_δ serán perpendiculares.

 

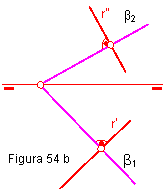
Por todo lo anterior, para trazar una recta perpendicular a un plano, bastará con que las trazas de la recta y las del plano sean perpendiculares. Figura 54 a y b.

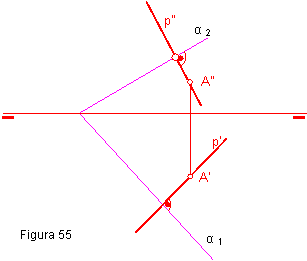
1.9.            TRAZAR POR UN PUNTOA UNA RECTA   p, PERPENDICULAR A UN PLANO α .

 

Bastará con trazar una recta perpendicular a las trazas del plano que y que pase el punto A. Figura 55.

1.10.   TRAZAR POR UN PUNTO  Q UN PLANO β PERPENDICULAR A UNA RECTA s.

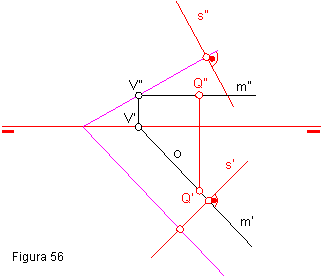
Por el punto  Q trazaremos una recta horizontal de plano  m (m’-m”), perpendicular a s’. Figura 56.

 

La traza del plano pasará por V” y será perpendicular a m”.

 

 

1.11.   PERPENDICULARIDAD ENTRE  DOS RECTAS.

 

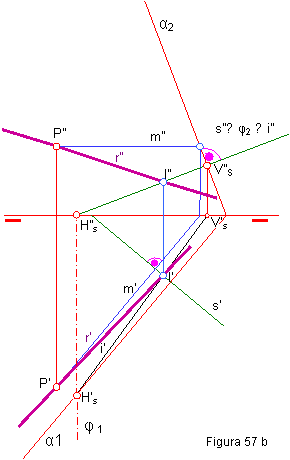
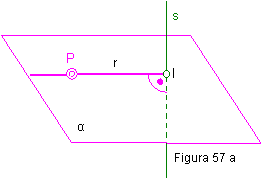
No existe a simple vista relación gráfica que nos permita ver la perpendicularidad entre dos rectas, tal y como podemos apreciar en la figura 57b.

Por tanto nos limitaremos a trazar una recta perpendicular a s que pase por un punto cualquiera P.

 

Elegimos un punto cualquiera P (P’-P”) y trazamos un plano perpendicular α(α₁-α₂) a  s (s’-s”). Ejercicio 57 a y b.

 

1. Hacemos contener a la recta s  en un plano proyectante vertical φ (φ ₁- φ ₂).

 

2. Hallamos la intersección de los planos α y β. Recta i(i’-i”). El punto I’-I”, será la intersección de la recta con el plano.

 

3. Uniendo I’-I” con P’-P”, tendremos la recta r(r’-r”), perpendicular a s(s’-s”).